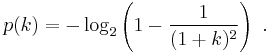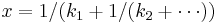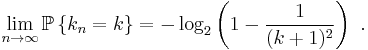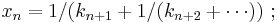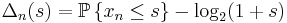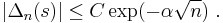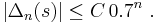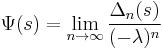Gauss–Kuzmin distribution

Gauss–Kuzmin
Parameters (none)
Support 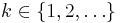k \in \{1,2,\ldots\}
PMF -\log_2\left[ 1-\frac{1}{(k%2B1)^2}\right]
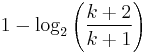CDF 1 - \log_2\left(\frac{k%2B2}{k%2B1}\right)
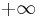Mean %2B\infty
Median 2\,
Mode 1\,
Variance 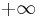%2B\infty
Skewness (not defined)
Ex. kurtosis (not defined)
Entropy 3.4325275...[1][2]

In mathematics, the Gauss–Kuzmin distribution is a discrete probability distribution that arises as the limit probability distribution of the coefficients in the continued fraction expansion of a random variable uniformly distributed in (0, 1).[3] The distribution is named after Carl Friedrich Gauss, who derived it around 1800,[4] and Rodion Kuzmin, who gave a bound on the rate of convergence in 1929.[5][6] It is given by the probability mass function

p(k) = - \log_2 \left( 1 - \frac{1}{(1%2Bk)^2}\right)~.

Contents

Gauss–Kuzmin theorem

Let

x = 1/(k_1 %2B 1/(k_2 %2B \cdots))

be the continued fraction expansion of a random number x uniformly distributed in (0, 1). Then

\lim_{n \to \infty} \mathbb{P} \left\{ k_n = k \right\} = - \log_2\left(1 - \frac{1}{(k%2B1)^2}\right)~.

Equivalently, let

x_n = 1/(k_{n%2B1} %2B 1/(k_{n%2B2} %2B \cdots))~;

then

\Delta_n(s) = \mathbb{P} \left\{ x_n \leq s \right\} - \log_2(1%2Bs)

tends to zero as n tends to infinity.

Rate of convergence

In 1928, Kuzmin gave the bound

|\Delta_n(s)| \leq C \exp(-\alpha \sqrt{n})~.

In 1929, Paul Pierre Lévy[7] improved it to

|\Delta_n(s)| \leq C \, 0.7^n~.

Later, Eduard Wirsing showed[8] that, for λ=0.30366... (the Gauss-Kuzmin-Wirsing constant), the limit

\Psi(s) = \lim_{n \to \infty} \frac{\Delta_n(s)}{(-\lambda)^n}

exists for every s in [0, 1], and the function Ψ(s) is analytic and satisfies Ψ(0)=Ψ(1)=0. Further bounds were proved by K.I.Babenko.[9]

See also

References

  1. ^ Blachman, N. (1984). "The continued fraction as an information source (Corresp.)". IEEE Transactions onInformation Theory 30 (4): 671–674. doi:10.1109/TIT.1984.1056924. 
  2. ^ Kornerup, P.; Matula, D. (July 1995). "LCF: A lexicographic binary representation of the rationals". Journal of Universal Computer Science 1: pp. 484–503. 
  3. ^ Weisstein, Eric W., "Gauss–Kuzmin Distribution" from MathWorld.
  4. ^ Gauss, C.F.. Werke Sammlung. 10/1. pp. 552–556. http://gdz.sub.uni-goettingen.de/dms/load/img/?PPN=PPN236018647. 
  5. ^ Kuzmin, R.O. (1928). "On a problem of Gauss". DAN SSSR: 375–380. 
  6. ^ Kuzmin, R.O. (1932). "On a problem of Gauss". Atti del Congresso Internazionale dei Matematici, Bologna 6: pp. 83–89. 
  7. ^ Lévy, P. (1929). "Sur les lois de probabilité dont dépendent les quotients complets et incomplets d'une fraction continue". Bullitin Societe Mathematique de France 57: pp. 178–194. JFM 55.0916.02. http://www.numdam.org/item?id=BSMF_1929__57__178_0. 
  8. ^ Wirsing, E. (1974). "On the theorem of Gauss–Kusmin–Lévy and a Frobenius-type theorem for function spaces". Acta Arithmetica 24: pp. 507–528. 
  9. ^ Babenko, K.I. (1978). "On a problem of Gauss". Soviet Math. Dokl. 19: pp. 136–140.